Optimization Algorithms
Transit Search Optimization Algorithm (2022)

Introduction
Welcome to the world of Transit Search (TS), a cutting-edge optimization algorithm that draws inspiration from the remarkable method of exoplanet detection known as transit. The TS presents a novel astrophysics-inspired meta-heuristic approach to solving complex scientific problems. With more than 3800 planets detected using the transit technique by space telescopes, this algorithm harnesses the power of transit exploration and adapts it to the realm of optimization.
The benefits of employing the TS algorithm in scientific research and problem-solving are manifold. Firstly, optimization lies at the heart of many scientific disciplines, from industrial internet of things to wireless networks, shape optimization of electric machines to vulnerability assessment of structures subjected to seismic activity. By leveraging TS, researchers can unlock new frontiers in their respective fields and achieve optimal solutions efficiently.
Unlike classical methods, which may guarantee optimal responses but struggle with complex and large-scale problems, meta-heuristic algorithms like TS excel in tackling such challenges. These algorithms may not guarantee finding the absolute best solution, but they excel in approximating optimal and acceptable answers within a reasonable timeframe. TS strikes a delicate balance between exploration and exploitation, employing innovative strategies inspired by the natural phenomena observed in exoplanet detection.
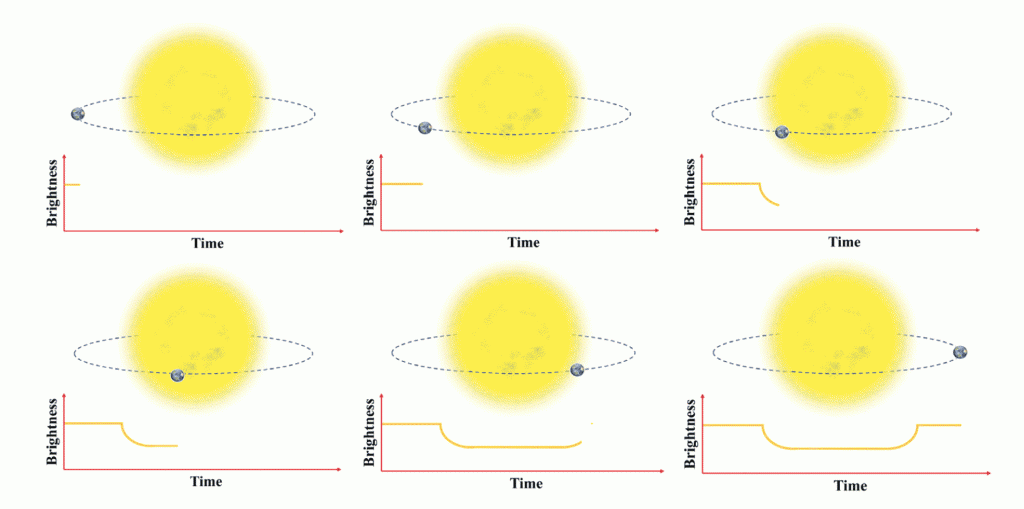
The Core of TS Algorithm
At its core, the transit algorithm analyzes the variations in luminosity observed when studying the light received from stars at specific intervals. A decrease in the amount of received light signifies the passage of a planet in front of the star, enabling its detection. Leveraging the efficiency and capabilities of the transit method in astrophysics, the researchers have ingeniously formulated an optimization technique that showcases exceptional performance.
Why TS algorithm?
The success of the TS algorithm can be attributed to several key factors. The algorithm’s exploration phase incorporates random strategies, galaxy phases, transit phases, planet phases, and neighbor phases, ensuring a comprehensive and efficient exploration of the search space. On the other hand, the exploitation phase fine-tunes the solutions obtained during exploration, optimizing their quality through the use of small noises and random parameters. This balance between exploration and exploitation, along with the algorithm’s ability to maintain multiple optimized solutions, enhances its robustness and performance. With its remarkable capabilities, TS is poised to revolutionize the field of optimization. By providing a comprehensive framework for solving a wide range of problems, this algorithm empowers researchers, engineers, and industries to address complex optimization challenges effectively. Its versatility, flexibility, and ability to deliver superior results make it a valuable tool in the scientific community.
Reference
Mirrashid, Masoomeh, and Hosein Naderpour. “Transit search: An optimization algorithm based on exoplanet exploration.” Results in Control and Optimization 7 (2022): 100127.
Links
IbI Logics Optimization Algorithm (2023)
Introduction
If you are looking for an effective optimization algorithm, the ILA is a good option to consider. The IbI Logics Algorithm (ILA) is a new optimization algorithm that is based on the theory of IbI logics. The ILA has three main phases: Exploration, Integration, and Exploitation. Each of the three phases of ILA is designed for a specific purpose. The Exploration phase is responsible for finding new solutions in the search space. The Integration phase is responsible for combining the new solutions with the existing solutions. The Exploitation phase is responsible for finding the best solution in the search space.
The ILA has several advantages over other optimization algorithms. First, the ILA can monitor the exploration and exploitation phases separately. This allows the user to control the performance of the algorithm and to adjust the parameters as needed. Second, the ILA is very accurate in determining the optimal solution. Third, the ILA has a reasonable computation time.
Here are some of the benefits of using the ILA optimization algorithm:
- The ILA can monitor the exploration and exploitation phases separately, which allows the user to control the performance of the algorithm and to adjust the parameters as needed.
- The ILA is very accurate in determining the optimal solution.
- The ILA has a reasonable computation time.
The Core of ILA
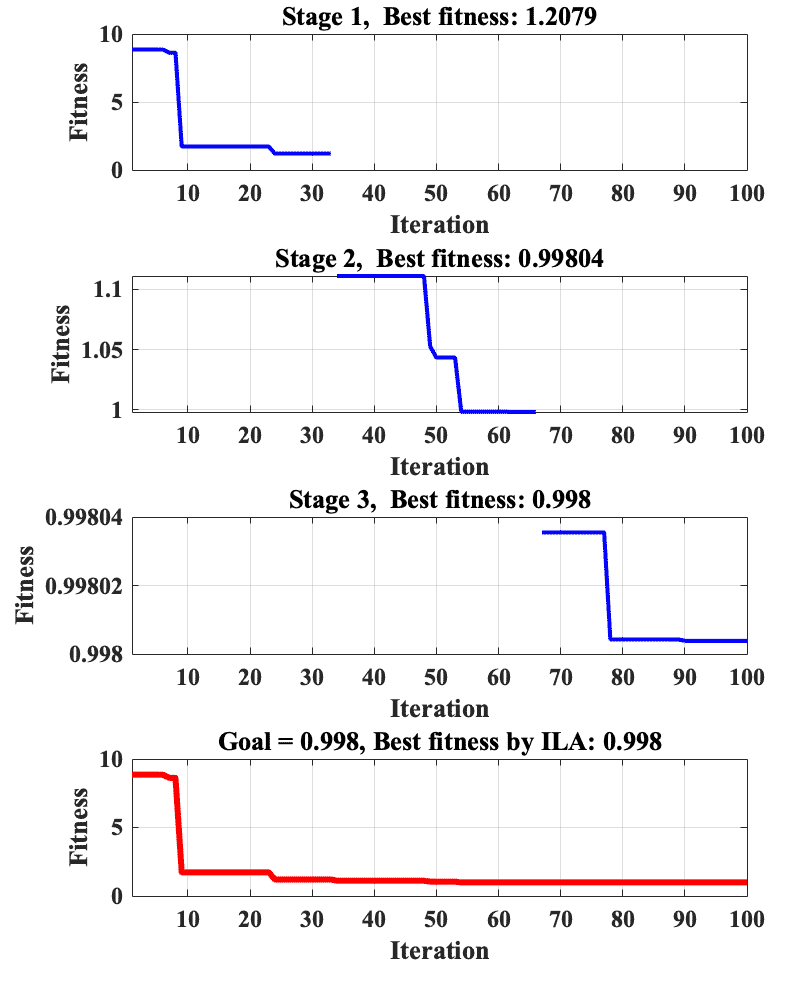
To illustrate the effectiveness of the IbI Logics Algorithm (ILA), we will delve into a specific benchmark problem known as the ‘De-Jong 5’. This benchmark problem is widely used in the field of optimization to evaluate the performance of various algorithms. The objective of the ‘De-Jong 5’ problem is to find the minimum value of a multimodal function within a given search space.
Let’s walk through the steps involved in applying the ILA to solve the ‘De-Jong 5’ problem:
Stage 1- Exploration Phase: In this phase, the ILA explores the search space by iteratively evaluating and updating the solutions. Through the exploration phase, the algorithm aims to identify promising regions within the search space that may contain optimal solutions.
Stage 2- Integration Phase: This phase focuses on integrating the information gathered during exploration and improving the experts’ performance. It combines the strengths of different experts to refine the solutions further.
- Stage 3- Exploitation Phase: In the exploitation phase, the ILA narrows down its focus to exploit the most promising regions identified in the exploration and integration phases. It intensifies the search in these regions, aiming to converge towards the optimal solution. By dedicating resources to exploit these regions, the algorithm maximizes its chances of finding the global minimum or an excellent near-optimal solution.
Reference
Mirrashid, Masoomeh., Naderpour, Hosein., “Incomprehensible but Intelligible-in-Time Logics: Theory and Optimization Algorithm”., (2023) Knowledge-Based Systems, 264, no. 110305., DOI: HTTPS://DOI.ORG/10.1016/j.knosys.2023.110305
